This is a write up for one of the FCSC (French Cyber Security Challenge) reverse engineering challenges.

It was the first time I had to deal with virtualized code, so my solution is far from being the best. Surely there were much quicker ways, but mine did get the job done. This write-up is essentially meant for beginners in the domain of obfuscated code reverse engineering.

Part 1: Type of challenge

This happens to be a keygen type of challenge, here are the rules (in French):

Basically, it is saying that you have to download a binary, that will take inputs, and much like a licensed software, will verify those inputs against each other. This is meant to mimic the way proprietary software verifies license keys.

The goal is the create a keygen: a script that will generate valid inputs to feed to the license verification algorithm. Of course, with only an offline validation, the challenge becomes trivial (simple patch and let’s goo), but you have to validate your inputs against an online version of the same binary. There are two inputs: a username, and a serial.

Executing it will yield:

 root@kali:~# ./keykoolol 
    [+] Username: toto
    [+] Serial:   tutu
    [!] Incorrect serial.

In those types of challenges, I would advise you to manually fuzz inputs. By sending special characters and strings with an invalid length, you might get an interesting error message. Keep in mind that the first step is the understand what the software is expecting as inputs.

But it’s not going to help here :) (would be too easy)

Let’s go roughly through the steps we will have to follow:

1. Download the binary
2. Disassemble it
3. Understand and implement the serial verification function
4. Implement an algorithm that, given an username, generates a corresponding serial
5. Test locally
6. Validate online
7. Get tons of points

Part 2: ELF analysis

The file is an 16Ko ELF file.

The command file gives:

keykoolol: ELF 64-bit LSB shared object, x86-64, version 1 (SYSV), dynamically linked, 
           interpreter /lib64/ld-linux-x86-64.so.2, for GNU/Linux 3.2.0, 
           BuildID[sha1]=1422aa3ad6edad4cc689ec6ed5d9fd4e6263cd72,
           stripped

Nothing tremendously interesting here, the sections though will reveal more interesting things (using readelf -e):

[14] .text             PROGBITS         0000000000000730  00000730
     0000000000001ce2  0000000000000000  AX       0     0     16
[16] .rodata           PROGBITS         0000000000002420  00002420
     00000000000004c0  0000000000000000   A       0     0     32
[24] .bss              NOBITS           0000000000203020  00003010
     0000000000002868  0000000000000000  WA       0     0     32

So text contains our code, but rodata and bss are quite large. 1216 bytes for rodata and 10Ko for bss ? Something smells fishy. As a reminder, bss is meant for uninitialized global variables. It often contains stuff like session encryption keys and pretty much any runtime data that requires a globally shared pointer.

What is in rodata ?

00000000: 0100 0200 5b2b 5d20 5573 6572 6e61 6d65  ....[+] Username
00000010: 3a20 000a 005b 2b5d 2053 6572 6961 6c3a  : ...[+] Serial:
00000020: 2020 2000 5b3e 5d20 5661 6c69 6420 7365     .[>] Valid se
00000030: 7269 616c 2100 5b3e 5d20 4e6f 7720 636f  rial!.[>] Now co
00000040: 6e6e 6563 7420 746f 2074 6865 2072 656d  nnect to the rem
00000050: 6f74 6520 7365 7276 6572 2061 6e64 2067  ote server and g
00000060: 656e 6572 6174 6520 7365 7269 616c 7320  enerate serials 
00000070: 666f 7220 7468 6520 6769 7665 6e20 7573  for the given us
00000080: 6572 6e61 6d65 732e 005b 215d 2049 6e63  ernames..[!] Inc
00000090: 6f72 7265 6374 2073 6572 6961 6c2e 0000  orrect serial...
000000a0: 0004 0000 0000 0000 0000 0000 0000 0000  ................
000000b0: 0000 0000 0000 0000 0000 0000 0000 0000  ................
000000c0: 6e18 b017 c9f5 bf08 7400 000a 3752 0a00  n.......t...7R..
000000d0: 9895 1c00 7403 0006 881c 0008 7400 000a  ....t.......t...
000000e0: 3f9e 0800 5694 1c00 ad06 180c c60f 2002  ?...V......... .
000000f0: 8802 0006 8997 0c00 7c02 080c c973 1c00  ........|....s..
00000100: 5b00 190c 7c00 0006 fa1b 0c00 f701 1000  [...|...........
00000110: a7f3 1f0c 4b19 100c fc00 0006 5a41 0c00  ....K.......ZA..
00000120: 0995 1c00 8e08 180c 280b 2602 e802 0006  ........(.&.....
00000130: 6434 7bff 050c 0002 afb4 68ff de24 f21a  d4{.......h..$..
00000140: 0588 f40c fd5c dd12 c049 df13 b982 d01d  .....\...I......

As expected, we can see the strings used by the binary to indicate us the validity of the entry. But what is after offset 0x000000c0 ? The data seems jibberish and not interpretable, but is it random ?

Let’s extract rodata segment using dd, and analyze its entropy with binwalk -E:

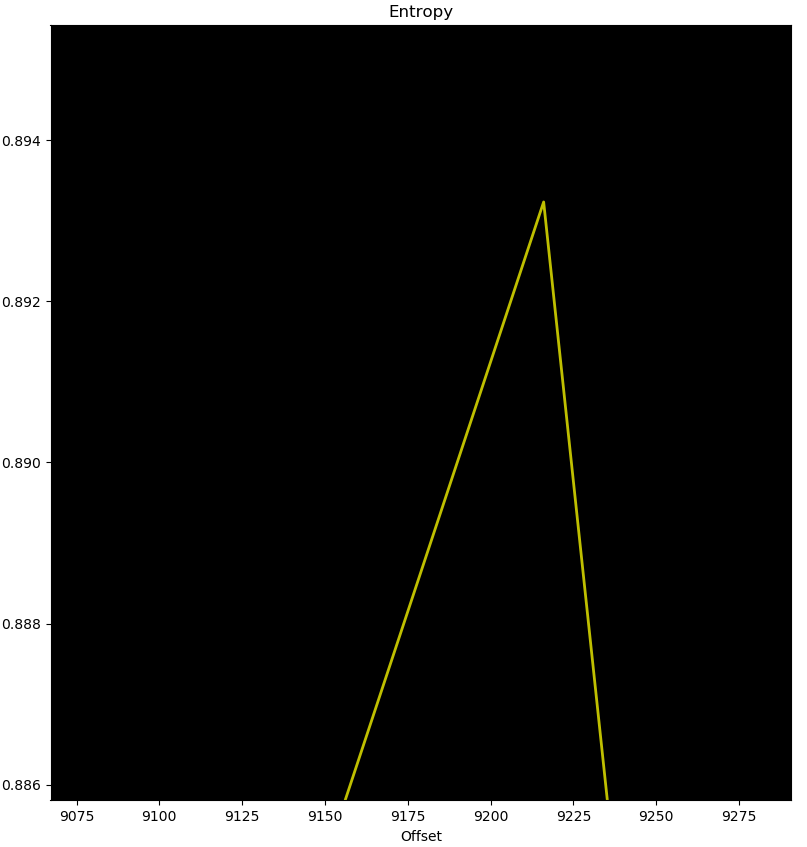
rodata’s entropy seems to be around 0.894; this is far not enough to qualify as random data. Though you probably already noticed that there were distingushable patterns in the sample. The NULL byte is very recurring, also the pattern 0006 appears four times, and 0c00 appears twice.

For instance, this is what the entropy of random data should look like:

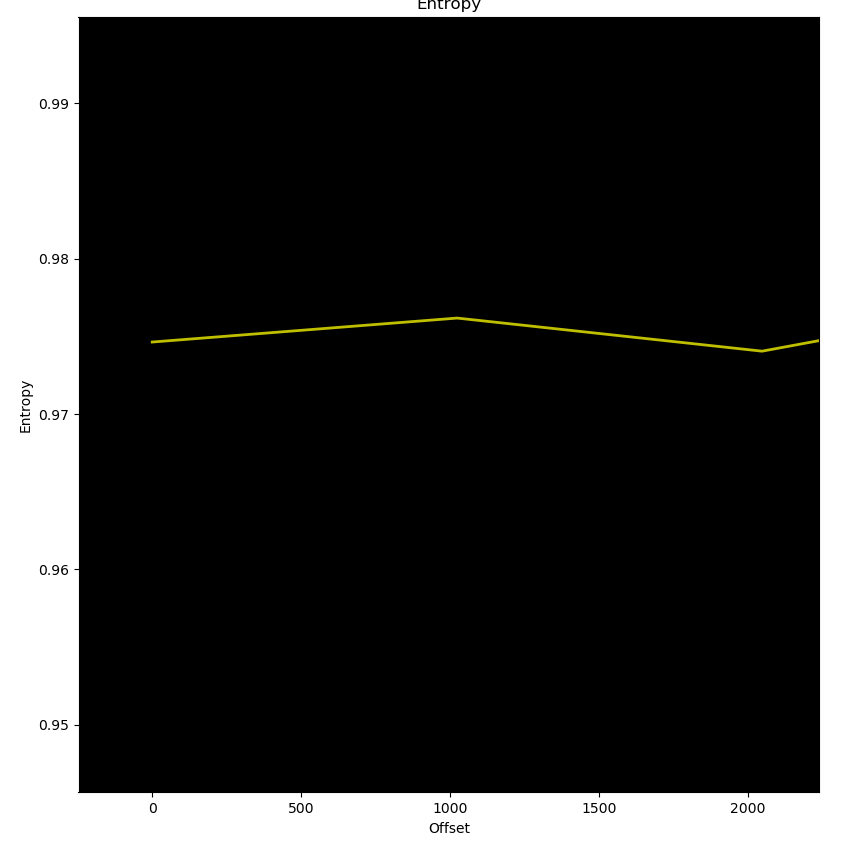
It’s slightly above 0.97, so there is a noticeable difference with the previous value.

Part 3: Binary disassembly

Let’s quickly examine the main function of the binary:

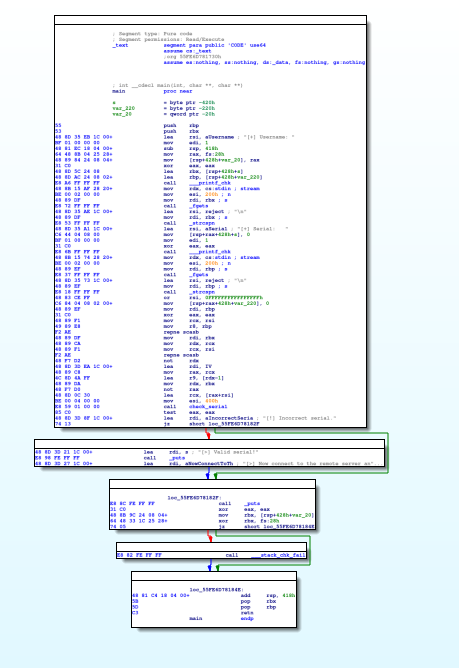
We can see a call to the function in charge of the serial’s validation, and then a conditional jump that will either print a valid response, or a negative one. There is no surprise here, we also can see those strings at the beginning of rodata.

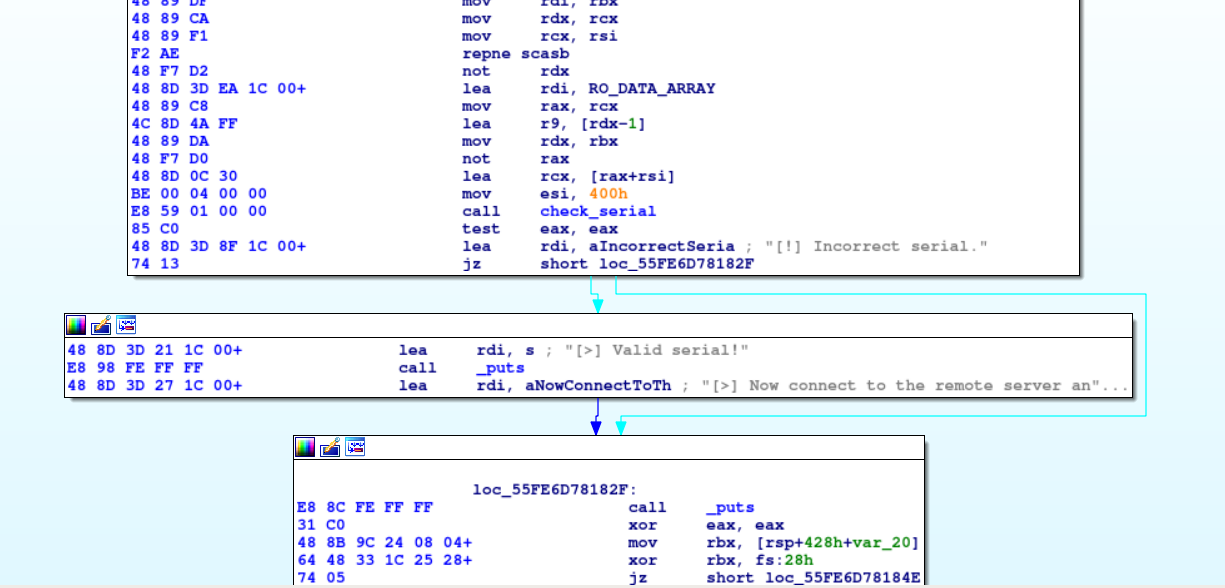
The interesting point here is that, if there was no online check (and that is a likely scenario with proprietary software), getting a valid prompt is as trivial as replacing a 0x74 JZ with a 0x75 JNZ after the validation function returns. But we will address micropatching in another post.

So now, to the main part ! Let’s reverse this check_serial function.

grazpfo#$eq!!!

OK I’m assuming that if you are still reading this it is because you are used to seeing horrible things in IDA (and I have come to learn since that this one is actually a nice one…).

Analyzing it’s parameters is going to help us understand what this is doing. It is taking the variable I named RO_DATA_ARRAY as an argument:

Guess who’s back ? It is indeed the segment we computed the entropy of earlier. RO_DATA_ARRAY is copied (0x400 bytes) in the bss (keep that in mind, it will make sense later). I will refer to the offset of RO_DATA_ARRAY’s copy in the bss by BSS_IR_ARRAY.

The main part of the validation function is actually a loop over all the values of this array, taken as dwords (4 bytes) and checking the value of the least significant byte.

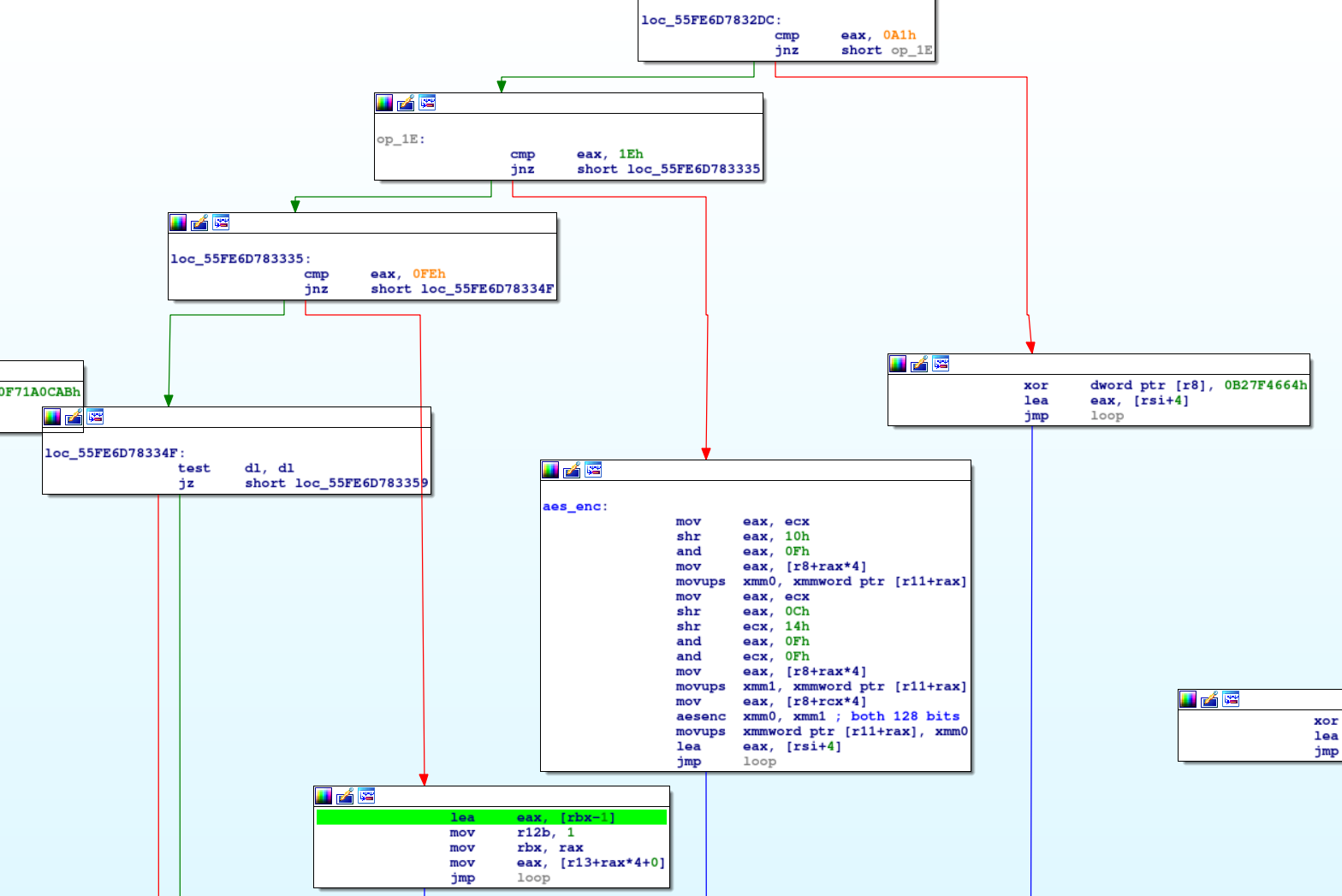
It is a 256 cases switch-case structure, and each different value for this byte will trigger a different code execution in the validation function.

Guess what’s going on here ?

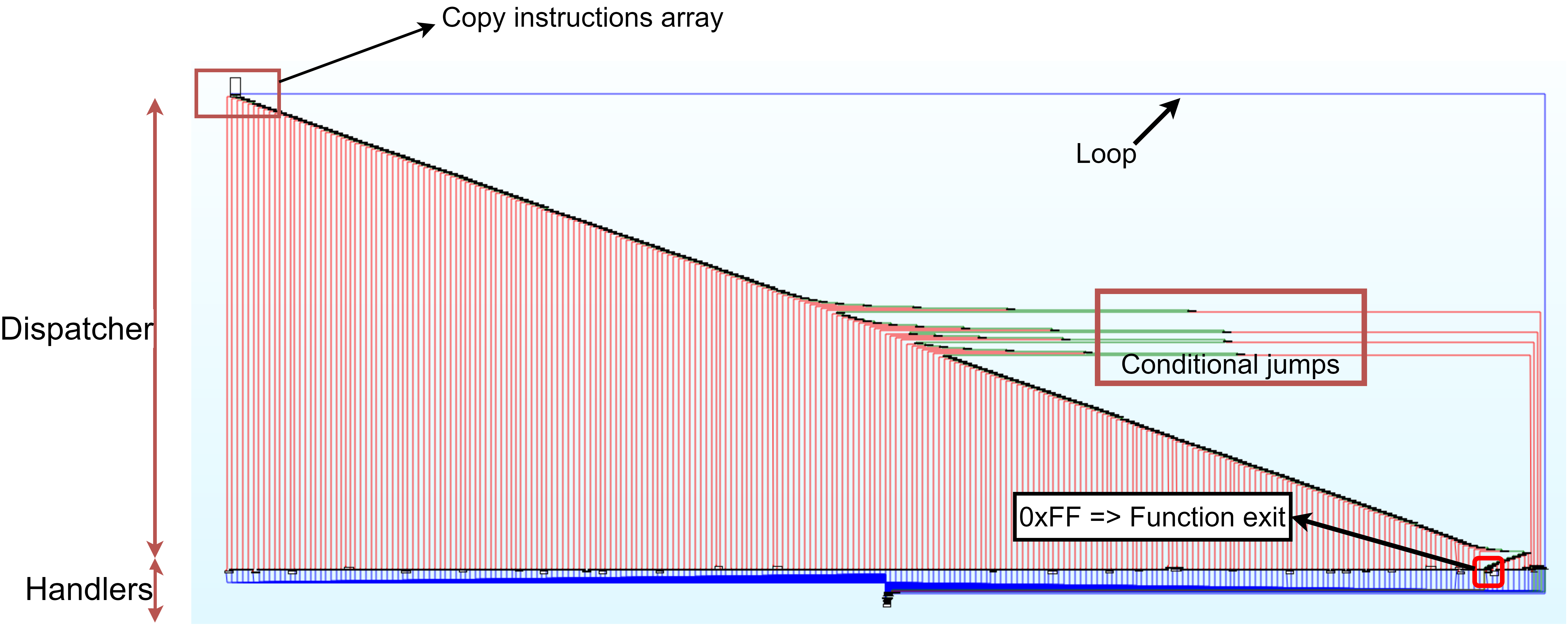
You are looking at a virtual processor, interpreting a custom byte code, also known as Intermediate Representation. The original code has been split in various basic blocks, and translated in another higher level code.

Let’s get a bit more into details:

• Dispatcher: It is parsing the intermediate representation, and linking each opcode with the code it is supposed to represent
• Handler: Contains the actual code executed for each instruction

Note the 4 branches that are put on the side by IDA, they have a very specific role: they are the only conditional jumps used by all the code. The code is somehow factorized, and that makes it a pain to place a breakpoint at a specific execution step.

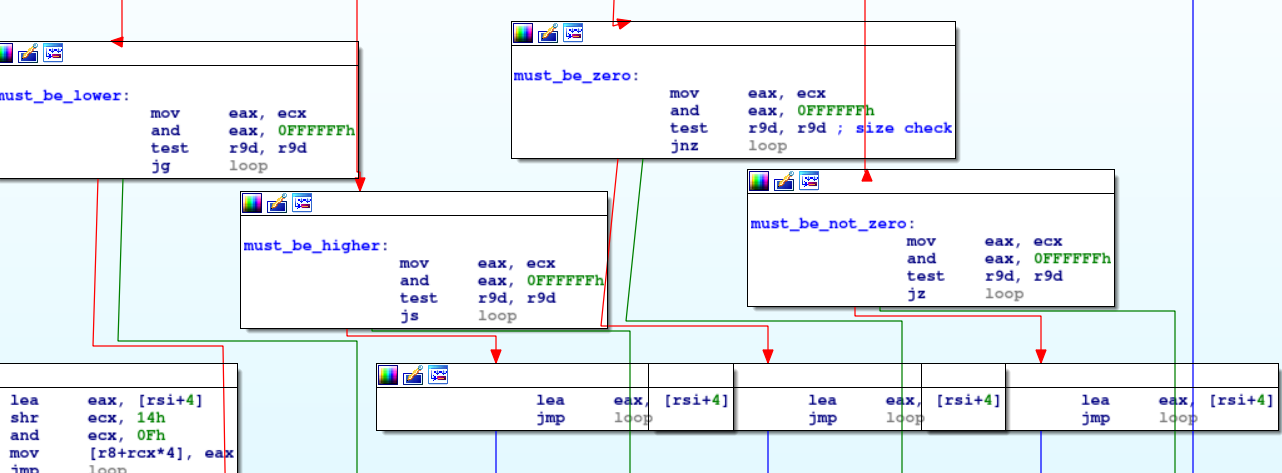
Please accept my most sincere apologies as I can clearly not organize an IDA graph in a clean way. I know it looks terrible but it’s the best I had…

Here is the IR to x86 translation for the conditional jumps:

• 15 : jump if greater (must be lower)
• 14 : jump if shorter (must be higher or equal)
• 0A : jump if not zero (must be equal)
• 09 : jump if zero (must be different)

Studying the IR, we start spotting coding patterns, here is an example:

    0x08401ca4 decrement r9d by 1
    0x090003d4 if r9d != 0, jump to 3d4, else, next
    0x0e210cb5 mul reg+a = c * reg+a
    0x00529386 increment int_val register
    0x180003e8 jump to 0F3554D7 (3e8)

This is the end of the loop that verifies the length of the input. Here we see two kinds of jumps: 08 09 is a sub, jz, and 18 is a jmp. This structure here 08 09 0e 00 18 marks the end of a for loop, with a goto.

The value it is initialized with is 0x100, so we know our serial should be 256 bytes long. Also, I wont be detailing it here, but the loop next to this one is checking every char in the serial against the regexp [0-9a-fA-F]*. So the actual length of the serial is 0x80, as we are supposed to input an hex encoded value

Doing this we learn two important things about the virtual machine:

1. The IR syntax
2. It’s macroscopic behaviour

Regarding the IR syntax, I did not completely understand all the instructions (00 to FF) but here is an example of IR syntax: Some instructions are in the form:

• iiaccxxx (stored 0xXXCXACIII) where:
• ii is the opcode (1 byte)
• rax <= a, dest address, located at BSS_IR_ARRAY+rax*4 (4 bits)
• rcx <= cc, source address, located at BSS_IR_ARRAY+rcx*4 (1 byte)
• xxx is the next instruction’s address (12 bits)

Addresses resolved by parameters a and c are in the bss section. There is a reason for that:

The bss actually contains the stack of our virtual machine ! And the part right before the beginning of the stack is understood by IDA as a section containing 2 bytes values, they are our registers !

Also ro_data is supposed to contain the code, but why copy the code to the stack then ? The answer lies is the next level of obfuscation: the code is self-modifying, hence the write permission requirement. Here is an example of a code block that is XORed:

0x1e53403a x l1' = enc(l6, l1)      | 0xca90f29b   
0x00303373                          | 0xd4f381d2
0x0c340d94                          | 0xd8f7bf35
0x00462b98                          | 0xd4859939
0x0c410a96                          | 0xd882b837
0x00575618                          | 0xd494e4b9
0x0c5508f0                          | 0xd896ba51

Right column contains the IR as it is in the ro_data segment, and left column is obtained after a XOR with 0xA1B2C3D4. So the opcodes d8, d4 etc are actually fake instructions sending you on a wrong path. They are dead code.

There are three steps of code XORing, pretty easily detectable once you were tricked by the first one, and after deobfuscating all the IR, here are the macro steps we obtain:

• STEP1: verify serial charset
• STEP2: hash username
• STEP3: decode new instructions with C1D2E3F4
• STEP4: decode hex serial
• STEP5: decode new instructions with A1B2C3D4
• STEP6: encrypt 32 rounds of AES
• STEP7: decode new instructions with AABBCCDD
• STEP8: loop over serial and verify value byte per byte

Part 3: Hashing the username

Let’s dig a bit deeper into the hashing function:

0x0e 3 0d 658 -> (username[i]+j)*0D
0x13 3 25 0e7 -> (username[i]+j)*0D ^ 25
0x11 3 ff 64b -> ((username[i]+j)*0D ^ 25) % FF => res

Here we can clearly see the syntax with the opcodes and parameters seen above: 0e is a multiplication, and the parameter c contains the value we multiply with. 13 is a xor with parameter c, and ff get the remainder of the euclidian division by parameter c. All those functions are applied to the value in the register in position 3 (value of parameter a).

This will compute the first 16 bytes line of the hash that will be derived in 5 other lines, totaling 96 bytes. I reimplemented the algorithm in python:

 def derived_key(tkey):
  s = tkey
  for k in xrange(0, 5):
          s += ''.join(chr(((ord(s[i+(k*16)])*0x03)^0xFF)&0xFF) for i in xrange(0,16))
  return s
            
def transient_key(username):
 temp = ('00'*16).decode('hex')
 for i in xrange(0, len(username)):
          temp2 = ''.join(chr((((ord(username[i])+j)*0x0D)^0x25)%0xFF) for j in xrange(0, 16))
          d = deque(temp2)
          d.rotate(i)
          temp = ''.join(chr(ord(temp[k])^ord(list(d)[k])) for k in xrange(0, 16))
 return temp

You’ll notice whoever imagined this loved circular shifts.

With a given username, you would obtain the same hash the binary computes using derived_key(transient_key(username)).

There is something pretty curious done at the end of this hashing algorithm. The binary copies the last two lines of the serial and appends them to the 96 bytes hash we just obtained. With an example input:

  * Username:           ecsc
  * Serial:             9f96d7f6380d729ffad1f09783706997
                        463911a0770040b6a78c0108563727fd
                        f4212b9de637638babe79c765c69238e
                        3e0205d228b9460c3857e112b84bb3ac
                        069421c9fca7e74a430c6526c0c53d71
                        bf8f00efb05897245041e27a7c564ea4
                        41414141414141414141414141414141
                        41414141414141414141414141414141

Here is a snapshot of the stack (bss but you get it) at the location that stores both the serial and the username’s hash:

In the box is the result of the hashing algorithm. Highlighted in yellow you can see the two lines of ‘A’s that were hex decoded, and appended to the end of the serial.

You can already tell that this input is not exactly randomly chosen, and I’ll explain why it looks like this.

Part 4: Crypto - where the fun starts

To summarize:

• The binary checks the serial, it must be a 0x80 bytes long hex encoded string
• The username is hashed, the result is 0x60 bytes long
• The last two lines are concatenated to this result, totaling 0x80 bytes

The reason those last two lines are treated differently is because they actually are an implicit parameter; they are encryption keys.

 Username:           ecsc
 Serial:             9f96d7f6380d729ffad1f09783706997
                     463911a0770040b6a78c0108563727fd
                     f4212b9de637638babe79c765c69238e
                     3e0205d228b9460c3857e112b84bb3ac
                     069421c9fca7e74a430c6526c0c53d71
                     bf8f00efb05897245041e27a7c564ea4
 Keys:               41414141414141414141414141414141
                     41414141414141414141414141414141

Once this hash is computed, the code encrypts the serial using AES-NI instruction aesdec for several rounds, and checks, byte per byte, that the decryption result is equal to the hash. The basic block realizing the encryption is here:

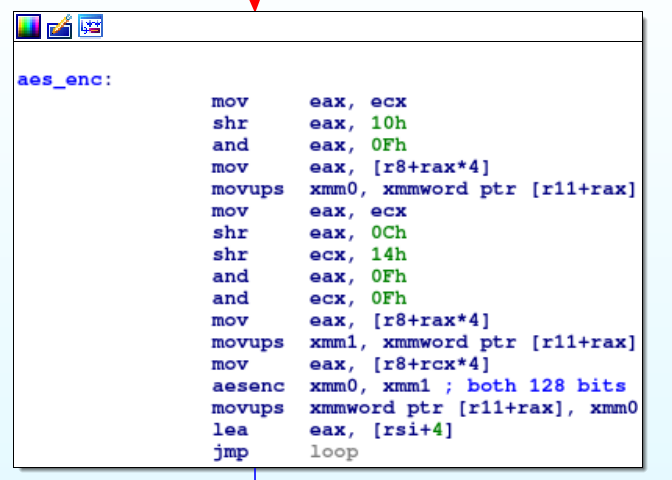
The xmm registers are 128 bits registers, so we are using AES 128. We will therefore name each 16 bytes line in the serial, as they will correspond to actual encryption blocks:

Username:           ecsc
Serial:             9f96d7f6380d729ffad1f09783706997 - l1
                    463911a0770040b6a78c0108563727fd - l2
                    f4212b9de637638babe79c765c69238e - l3
                    3e0205d228b9460c3857e112b84bb3ac - l4
                    069421c9fca7e74a430c6526c0c53d71 - l5
                    bf8f00efb05897245041e27a7c564ea4 - l6
Keys:               41414141414141414141414141414141 - k1
                    41414141414141414141414141414141 - k2

We are then looking for a serial verifying: serial == decrypt(hash, key)

Now the encryption algorithm itself is based on AES single round, but the block chaining is entirely custom, and uses circular shifts (hey you again). One round of this block encryption looks like this:

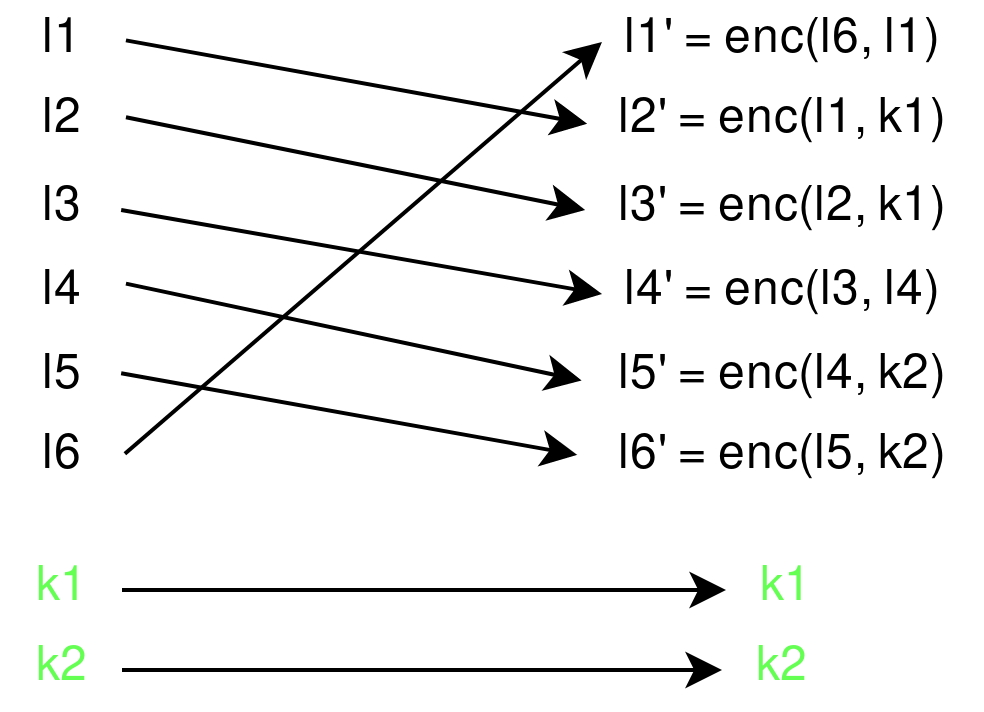
You can already guess that the order of decryption is going to be very important, as some round keys will be encrypted.

To test this, round by round, I have implemented a very simple x64 code (that will segfault but is meant to be debugged to get the register’s values):

section .text
    global _start       
_start:                     
    mov rax, 0x4141414141414141
    movq xmm0, rax
    mov rax, 0x4141414141414141 
    pinsrq xmm0, rax, 1
    mov rax, 0x1010101010101010
    movq xmm1, rax
    mov rax, 0x1010101010101010
    pinsrq xmm1, rax, 1
    aesdec xmm0, xmm1
    ret

This will encrypt with one single round of AES the string 0x41414141414141414141414141414141 with the key 0x10101010101010101010101010101010.

Now, part of the problem is to implement, or find, an AES program that will allow you to encrypt or decrypt with single rounds of AES. You can’t do that with OpenSSL or PyCrypto as the number of rounds is standardized and depends on the key size (10 round for AES 128 in this case).

A simple encryption round for AES looks like:

def aes_round(self, state, roundKey):
        state = self.subBytes(state, False)
        state = self.shiftRows(state, False)
        state = self.mixColumns(state, False)
        state = self.addRoundKey(state, roundKey)
        return state

So obviously the inverse would be:

def aes_invRound(self, state, roundKey):
        state = self.addRoundKey(state, roundKey)
        state = self.mixColumns(state, True)
        state = self.shiftRows(state, True)
        state = self.subBytes(state, True)
        return state

Using the inverse round, we implement what corresponds to:

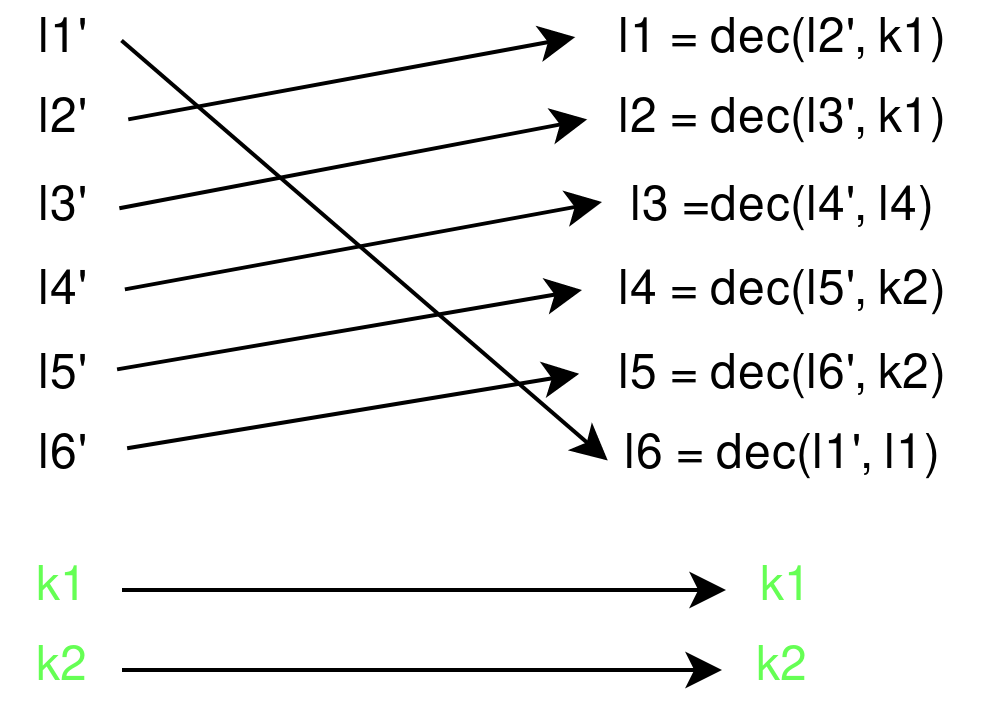
Bear in mind that this is one single round of block encryption, the custom chaining actually performs 32 rounds of it. But you get the idea.

It is very important to note here, that l6 cannot be decrypted before l1, as it needs the decrypted value of l1. The same goes for l3, that relies on l4. All the other lines are decrypted using k1 and k2.

Once we have this algorithm, our main keygen function should look like this:

 generate_serial(username, key):
    hash username
    decrypt hash using key, 32 times
    return result

And of course:

root@kali# cat input | ./keykoolol 
[+] Username: [+] Serial:   [>] Valid serial!
[>] Now connect to the remote server and generate serials
for the given usernames.

!!

Part 5: If you do it, be smarter than me

The alternatives that would have spared me a lot of time placing uncertain breakpoints are:

• Symbolic execution (using angr, miasm or whatever you like)
• Translating the whole intermediate representation through automation

I didn’t try those methods, but people who used them definitely had quicker results, so I think about exploring them in further posts.

Resources

Pure python aes

Reversing a virtual machine

That’s it for today, I hope you enjoyed it.

Stay classy netsecurios.

Reverse Engineering Obfuscated Code

FCSC 2020 Keykoolol 500 points —